Interactions of statistical physics with other fields
Research interests
I am interested in the interplay between statistical mechanics and other fields, including number theory and the ergodic and geometric aspects of group theory. My favourite model of statistical mechanics is percolation, which simply consists in keeping or erasing each elementary constituent of your geometric medium independently with some retention probability \(p\). There is a critical value for \(p\), which is called \(p_c\). Below this critical value, the medium breaks into dust while above it, the medium keeps its properties. This phenomenon is strongly related to the phase transitions encountered in physics.
Locality beyond \(p_c\)
with Christoforos Panagiotis
Given only a large ball of a homogeneous graph \(\mathcal{G}\) of superlinear polynomial growth, we obtain a fine understanding of supercritical percolation on \(\mathcal{G}\).
ArXiv, 2025

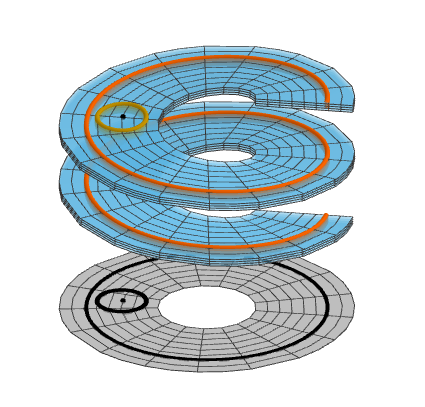
Arithmetic percolation
with Samuel Le Fourn and Mike Liu
We study the white connected components and the black connected components of the random colouring you see in the picture. We also do so for other lattices and in higher dimension.
ArXiv, 2025

Stochastic domination and lifts
with Rémy Poudevigne--Auboiron and Paul Rax
On a chessboard, toss one coin per column and, when you get heads, put a pawn somewhere in that column. How does it compare with tossing one coin per square and putting pawns accordingly?
ArXiv, 2025
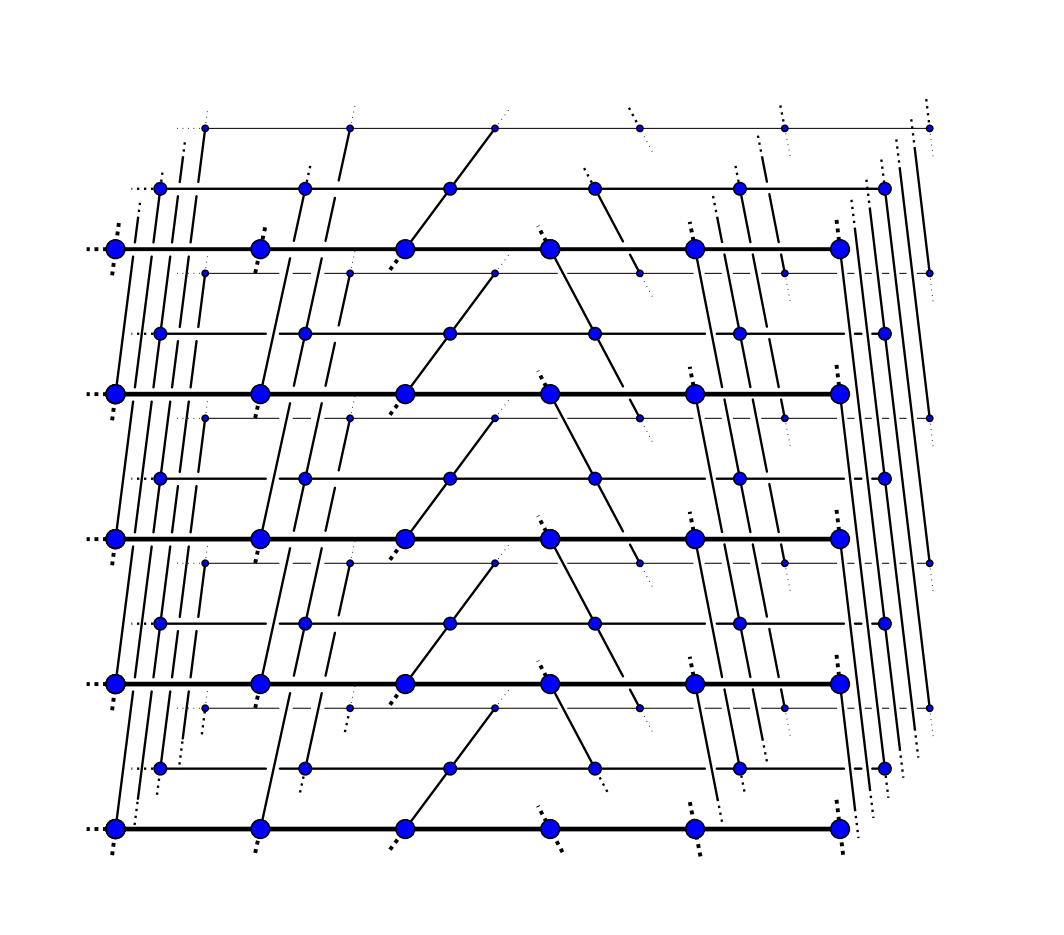
Supercritical percolation
with Daniel Contreras and Vincent Tassion
We study supercritical percolation on homogeneous graphs of polynomial growth.
Duke Mathematical Journal, 2024
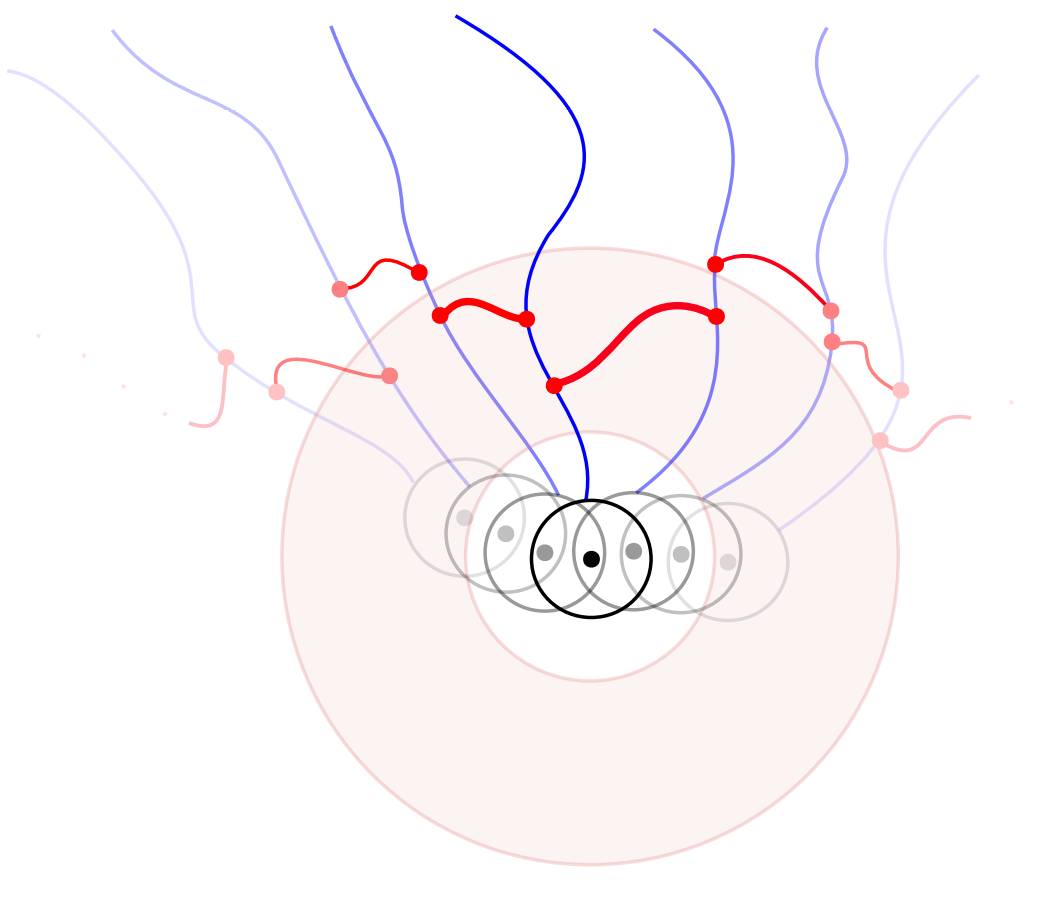
Polynomial locality
with Daniel Contreras and Vincent Tassion
Using this companion paper, we prove Schramm's Locality Conjecture under the assumption of polynomial growth.
Electronic Communications in Probability, 2023

The random coprime colouring
Plant a forest with one thin tree at each vertex of \(\mathbb{Z}^d\). Then pick a tree "uniformly at random" and replace it by a lamp. Which are the trees lit by the lamp?
Electronic Communications in Probability, 2022
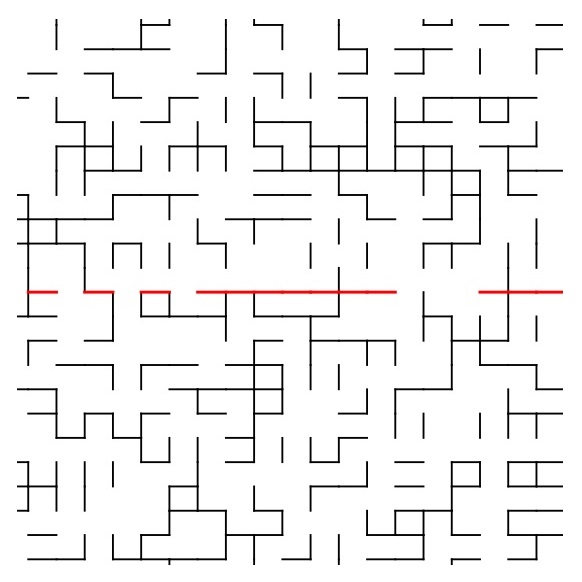
Inhomogeneous percolation
with Bernardo de Lima, Humberto Sanna, and Daniel Valesin
We investigate percolation on \(\mathbb{Z}^d\) with a sublattice of defects.
ALEA, 2022
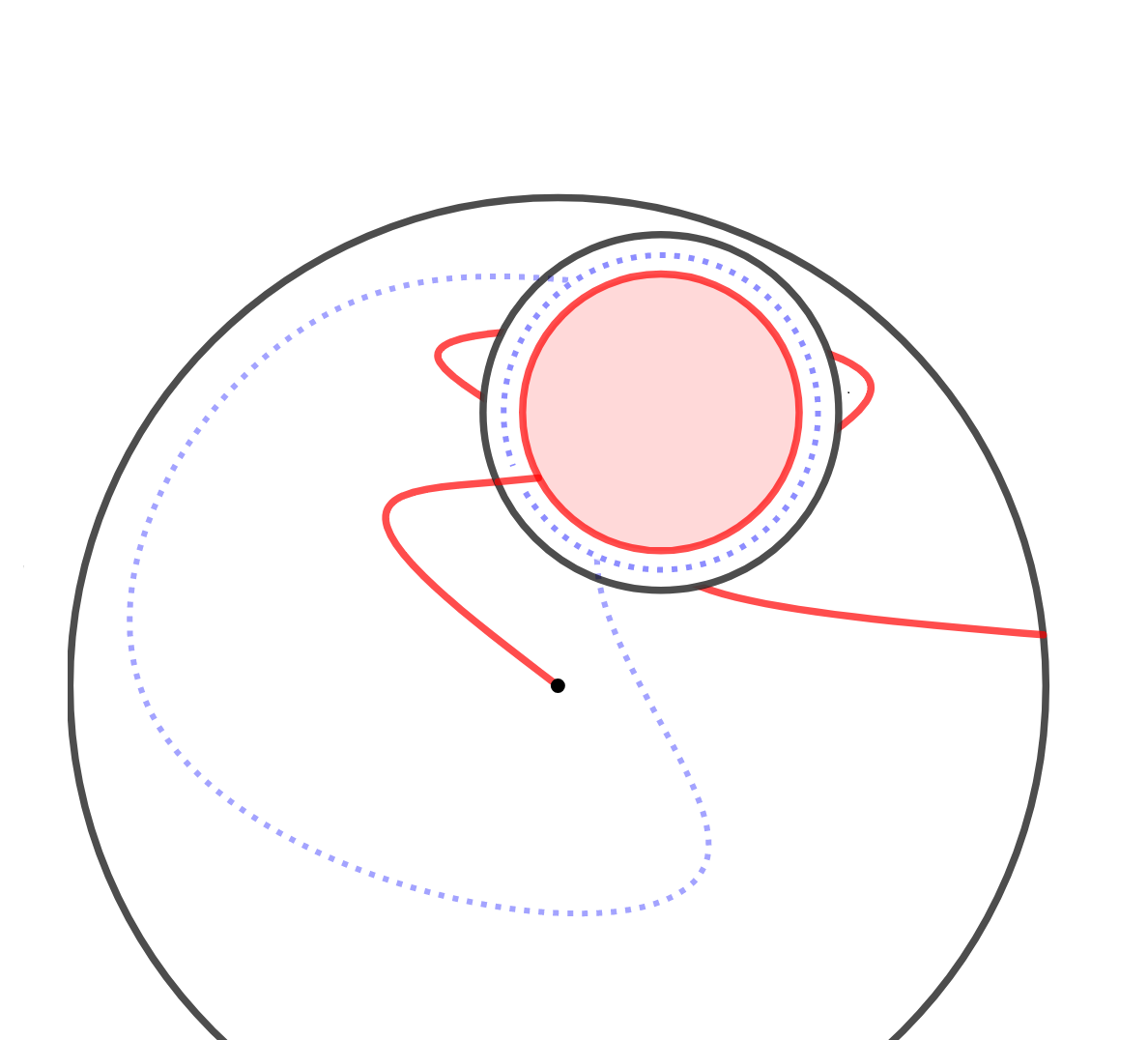
Strict monotonicity
with Franco Severo
We show that taking strict quotients of graphs with \(p_c<1\) strictly increases the value of \(p_c\). This answers Question 1 of the Percolation beyond \(\mathbb{Z}^d\) paper of Benjamini and Schramm.
Annals of Probability, 2019
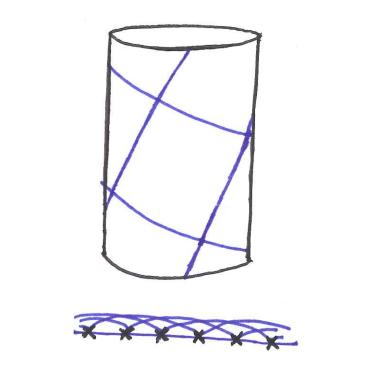
Abelian locality
with Vincent Tassion
We prove Schramm's Locality Conjecture in the particular case of Cayley graphs of abelian groups.
Annals of Probability, 2017
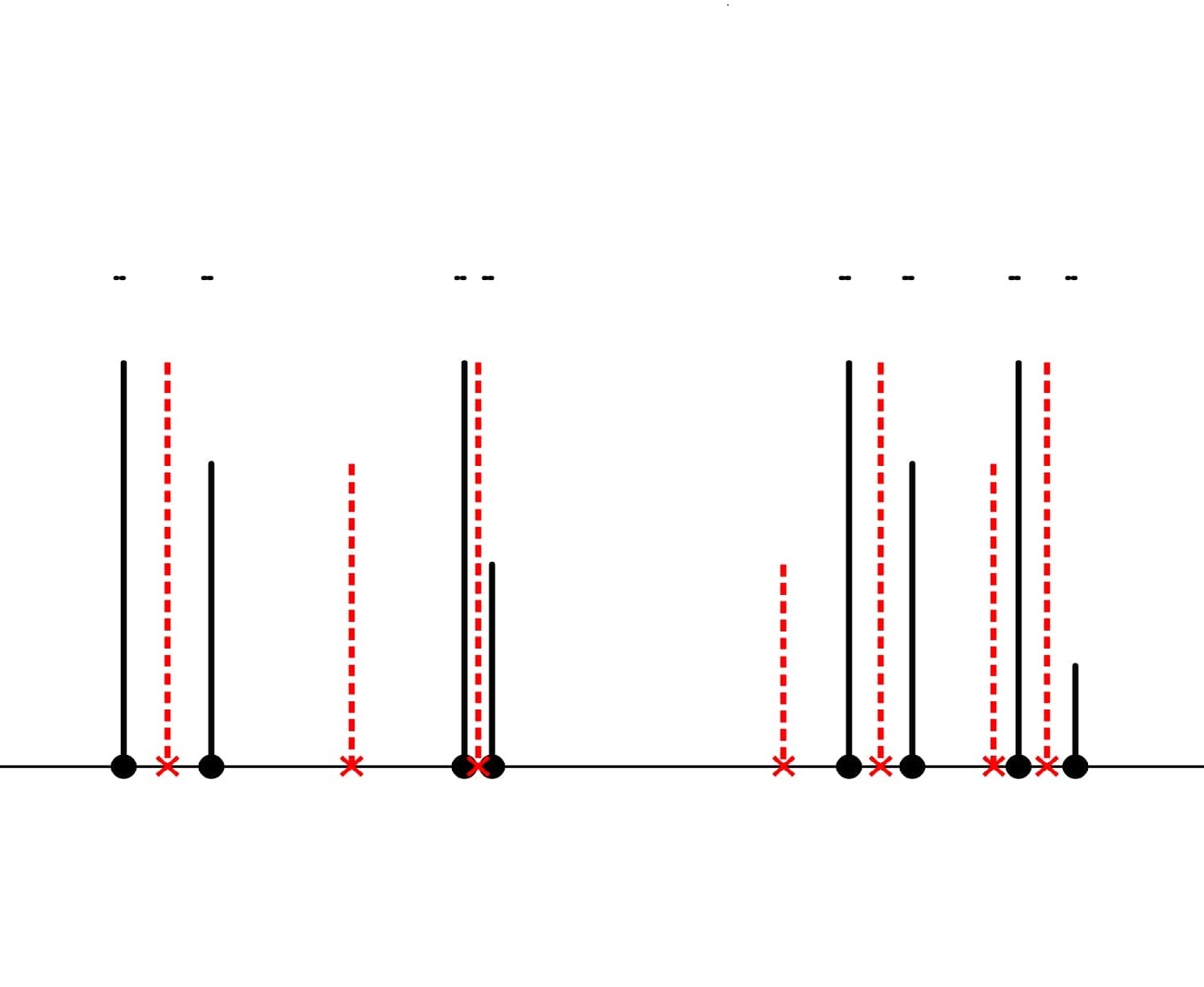
Many connective constants
This article proves that the set of connective constants of Cayley graphs contains a Cantor set.
Electronic Communications in Probability, 2017

Directed DLA
This paper investigates a model midway between ballistic deposition and diffusion-limited aggregation.
ALEA, 2017
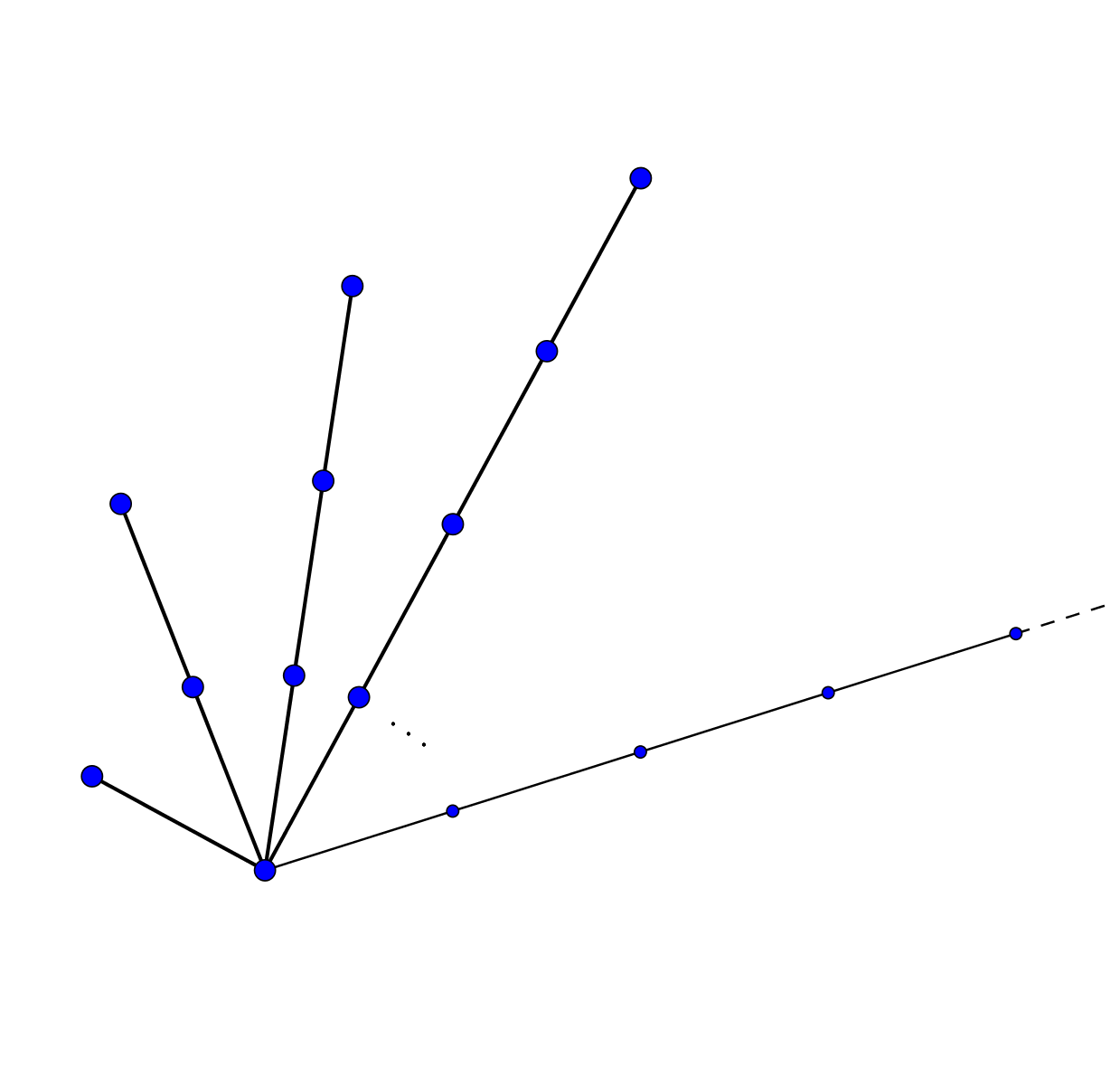
Locally infinite graphs
This paper investigates the geometry of homogeneous locally infinite graphs.
The Graduate Journal of Mathematics, 2017
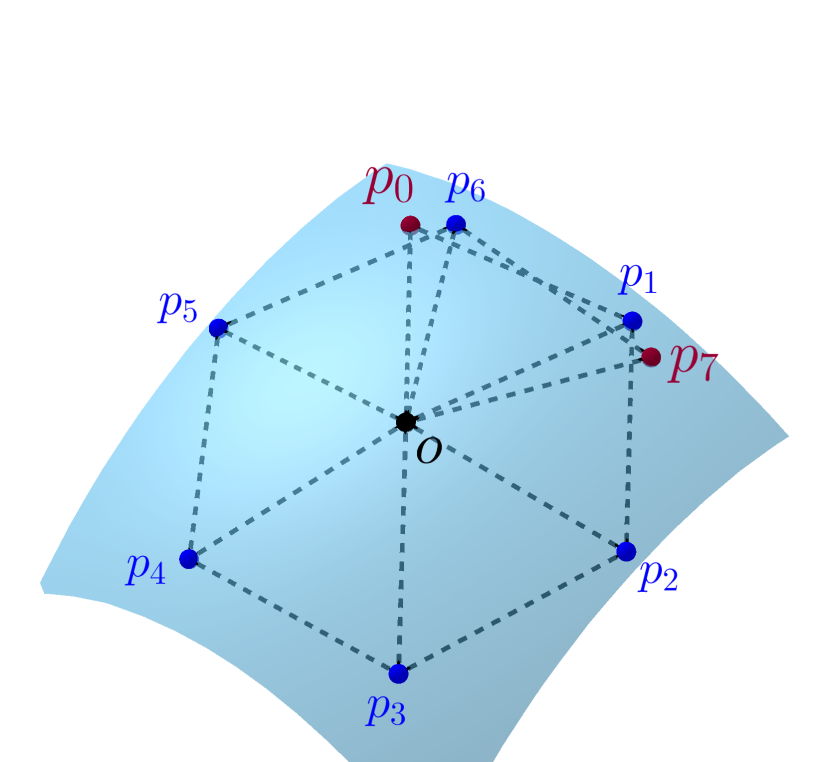
Rotarily transitive graphs
Cayley graphs are graphs that are homogeneous due to translations. Can a graph be homogeneous due to rotations?
ArXiv, 2016
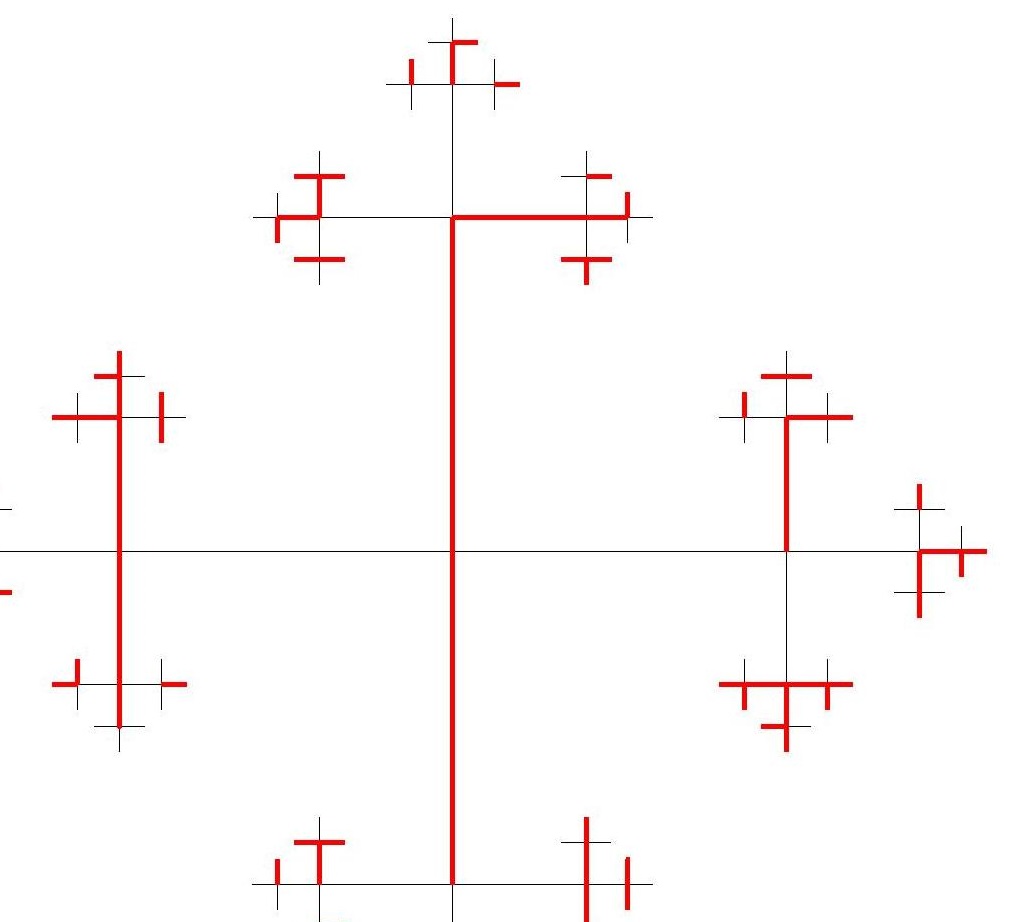
Ergodicity and indistinguishability
We review the dictionary translating between orbit equivalence and percolation, and add a new word to it.
L'Enseignement Mathématique, 2015